Deriving the Small-Signal Equation of a Buck Converter

When designing a control strategy for an electronic circuit we have to be able to model the circuit in mathematical expression. This time I will show how to derive a mathematical expression of the input and output of a buck converter circuit.

This time we just simply use KCL and KVL to derive the mathematical expression of the Buck converter.

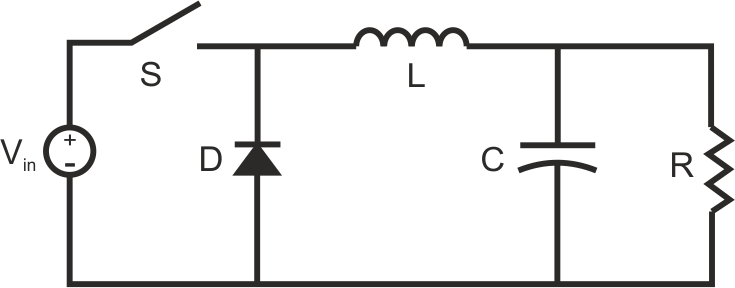
The picture above is the simplified circuit of a buck converter. The switching device, Transistor, is replaced with a simple on-off switch for simplicity.

Now we will analyze the circuit based on the state of the switching device. First, let’s analyze when the switch S is close then the diode D will be reverse biased. The circuit’s current and voltage are described in the picture below.

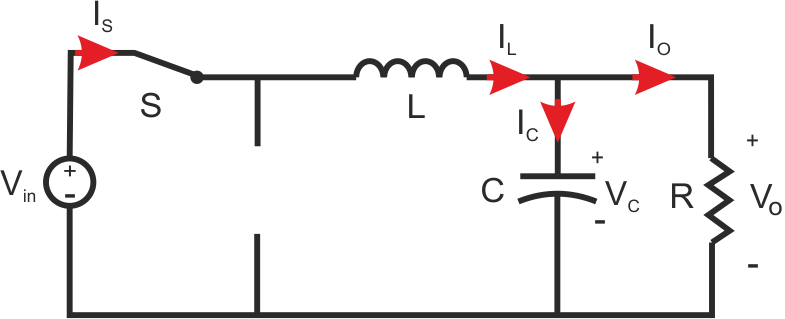
State I, 0< t <dT_s

$L\frac{d{i}_{L}}{dt} = {v}_{in} - {v}_{o}$

$C\frac{{v}_{c}}{dt} = {i}_{L} - {i}_{o}$

${v}_{o} = {v}_{c}$

Now, let’s analyze the circuit when switch S is open and this time the diode D will be forward-biased. The circuit’s current and voltage are described in the picture below.

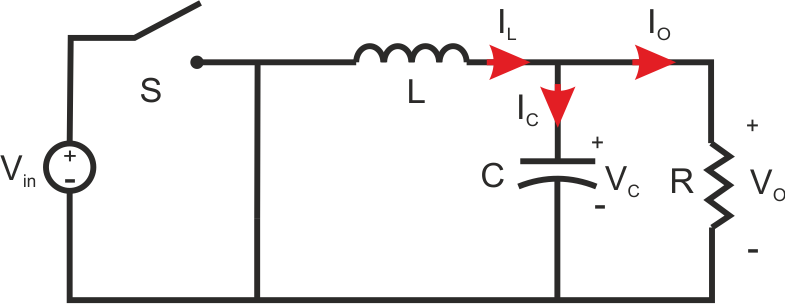
State II, dT_s< t <T_s

$L\frac{d{i}_{L}}{dt} = - {v}_{o}$

$C\frac{{v}_{c}}{dt} = {i}_{L} - {i}_{o}$

${v}_{o} = {v}_{c}$

The next step is calculating the averaged differential equations over one switching cycle.

$L\frac{d{i}_{L}}{dt} = d\left({v}_{in}- {v}_{o}\right) + \left(1- d\right)\left(- {v}_{o}\right)$

$L\frac{d{i}_{L}}{dt} = d{v}_{in}- {v}_{o}$

$C\frac{d{v}_{c}}{dt} = d\left({i}_{L} - \frac{{v}_{o}}{R}\right) + \left(1 - d\right)\left({i}_{L} - \frac{{v}_{o}}{R}\right)}$

$C\frac{d{v}_{c}}{dt} = {i}_{L} - \frac{{v}_{o}}{R}$

${v}_{o} = d\left({v}_{c}\right) + \left(1 - d\right)\left({v}_{c}\right)$

${v}_{o} = {v}_{c}$

As can be seen from the equation above the term dv_in contains both the input v_in and the control variable d, so the classical control theory cannot be implemented. In order to get a linear model we need to apply a perturbation on each variable. The idea is on the steady state we assume that each of these variables will contain a DC component and a small AC component. The equation before will be like below.

$L\frac{d\left({I}_{L} + {\widetilde{i}}_{L}\right)}{dt} = \left(D + \widetilde{d}\right)\left({V}_{s} + {\widetilde{v}}_{s}\right) - \left({V}_{o} + {\widetilde{v}}_{o}\right)$

$L\frac{d{\widetilde{i}}_{L}}{dt} = \underset{dc}{D{V}_{s}} + \underset{ss}{D{\widetilde{v}}_{s}} + \underset{ss}{\widetilde{d}{V}_{s}} + \underset{ho}{\widetilde{d}{\widetilde{v}}_{s}} - \underset{dc}{{V}_{o}} - \underset{ss}{{\widetilde{v}}_{o}}$

$C\frac{d\left({V}_{c} + {\widetilde{v}}_{c}\right)}{dt} = \left({I}_{L} + {\widetilde{i}}_{L}\right) - \frac{1}{R}\left({V}_{o} + {\widetilde{v}}_{o}\right)$

$C\frac{d{\widetilde{v}}_{c}}{dt} = \underset{dc}{{I}_{L}} + \underset{ss}{{\widetilde{i}}_{L}} - \underset{dc}{\frac{{V}_{o}}{R}} - \underset{ss}{\frac{{\widetilde{v}}_{o}}{R}}$

${V}_{o} + {\widetilde{v}}_{o} = {V}_{c} + {\widetilde{v}}_{c}$

${\widetilde{v}}_{o} = \underset{dc}{{V}_{c}} + \underset{ss}{{\widetilde{v}}_{c}}$

Note:
dc means the DC component
ss means the small-signal component
ho means the high-order component

From the equations above we can extract the DC component which will be useful to analyze the circuit at steady-state and we can also extract the AC small-signal component as well which then will be used to design our control strategy.

First, let’s extract the DC component.

$0 = D{V}_{s} - {V}_{o}$

$0 = {I}_{L} - \frac{{V}_{o}}{R}$

${V}_{c} = {V}_{o}$

Note :
At steady-state
The inductor voltage = 0
The capacitor current = 0

Now, let’s see what we have for the small-signal component

$L\frac{d{\widetilde{i}}_{L}}{dt} = D{\widetilde{v}}_{s} + \widetilde{d}{V}_{s} - {\widetilde{v}}_{o}$

$C\frac{d{\widetilde{v}}_{c}}{dt} = {\widetilde{i}}_{L} - \frac{{\widetilde{v}}_{o}}{R}$

${\widetilde{v}}_{o} = {\widetilde{v}}_{c}$

The next step is to apply the Laplace transformation to our small-signal equations in order to express them in the frequency domain.

$sL{\widetilde{i}}_{L}\left(s\right) = D{\widetilde{v}}_{s}\left(s\right) + \widetilde{d}\left(s\right){V}_{s} - {\widetilde{v}}_{o}\left(s\right)$

$sC{\widetilde{v}}_{c}\left(s\right) = {\widetilde{i}}_{L}\left(s\right) - \frac{{\widetilde{v}}_{o}}{R}\left(s\right)$

${\widetilde{v}}_{o}\left(s\right) = {\widetilde{v}}_{c}\left(s\right)$

Now, we can perform the algebra to eliminate the v_c(s) and i_L(s). First, we can rearrange the second equation to express the i_L(s) as the equation below.

$sC{\widetilde{v}}_{c}\left(s\right) = {\widetilde{i}}_{L}\left(s\right)- \frac{{\widetilde{v}}_{o}}{R}\left(s\right)\rightarrow {\widetilde{i}}_{L} = sC{\widetilde{v}}_{c}\left(s\right) + \frac{{\widetilde{v}}_{o}}{R}\left(s\right)$

Now, we substitute it to the first equation then we will get the first equation as below,

$sL\left(sC{\widetilde{v}}_{c}\left(s\right) + \frac{{\widetilde{v}}_{o}}{R}\left(s\right)\right) = D{\widetilde{v}}_{s}\left(s\right) + \widetilde{d}\left(s\right){V}_{s} - {\widetilde{v}}_{o}\left(s\right)$

Finally, we can express the output as:

${\widetilde{\boldsymbol v}}_{\boldsymbol o}\left(\boldsymbol s\right) = \frac{\boldsymbol D{\widetilde{\boldsymbol v}}_{\boldsymbol s}\left(\boldsymbol s\right) + \widetilde{\boldsymbol d}\left(\boldsymbol s\right){\boldsymbol V}_{\boldsymbol s}}{\boldsymbol L\boldsymbol C\boldsymbol s^2 + \frac{\boldsymbol L}{\boldsymbol R}\boldsymbol s + 1}$

For our control design, we will need the control-to-output transfer function which is expressed as the equation below.

${\left(\frac{{\widetilde{\boldsymbol v}}_{\boldsymbol o}\left(\boldsymbol s\right)}{\widetilde{\boldsymbol d}\left(\boldsymbol s\right)}\right)}_{{\widetilde{\boldsymbol v}}_{\boldsymbol s} = 0} = \frac{{\boldsymbol V}_{\boldsymbol s}}{\boldsymbol L\boldsymbol C\boldsymbol s^2 + \frac{\boldsymbol L}{\boldsymbol R}\boldsymbol s + 1}$