Deriving the Small-Signal Model of the Boost Converter using State-Space Averaging

The small-signal model is so handy in predicting the behavior of the non-linear system. But sometimes the process of deriving the small-signal model equation can be a tedious work. In that case we can construct a MATLAB script to do the calculation.

Here is the MATLAB script that I made for obtaining the control-to-output transfer function of non-ideal Boost converter.

SSA_Boost_for_MATLAB Download

1. Identify the amount of capacitor and the inductor on the DC-DC converter circuit. Each of these energy storage elements will be the space vector of the matrix.

In this Boost converter circuit, there are two energy storage elements (one inductor and one capacitor). In that case, there will be two state vectors on our matrix (iL, vC).

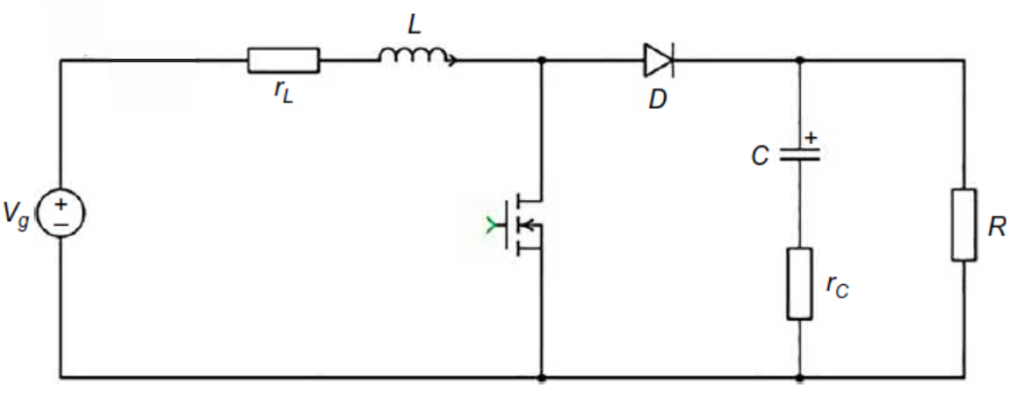
2. Write down the equation for each state vector for each half cycle.
The MOSFET is on while the diode is off, DTs.

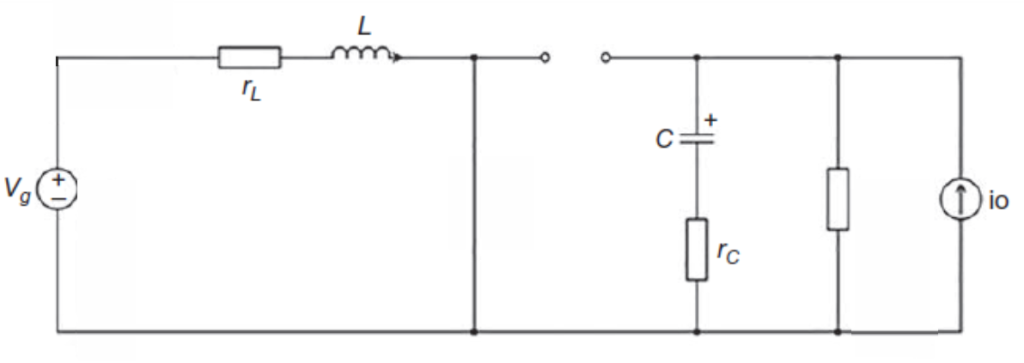
$\begin{align*} \frac{d{i}_{L}\left(t\right)}{dt} &= \frac{1}{L}\left( - {r}_{L}{i}_{L} + {v}_{g}\right) \\ \\ \frac{d{v}_{C}\left(t\right)}{dt} &= \frac{1}{C}\left( - \frac{1}{R + {r}_{C}}{v}_{C}\right) \\ \\ {v}_{O} &= \frac{R}{R + {r}_{C}}{v}_{C} \end{align*}$

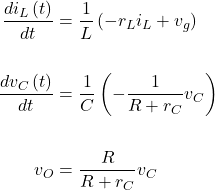
The MOSFET is off while the diode is on, (1-D)Ts.

$\begin{align*} \frac{d{i}_{L}\left(t\right)}{dt} &= \frac{1}{L}\left(- \left({r}_{L} + \frac{R \times {r}_{C}}{R + {r}_{C}}\right){i}_{L}- \frac{R}{R + {r}_{C}}{v}_{C} + {v}_{g}\right) \\ \\ \frac{d{v}_{C}\left(t\right)}{dt} &= \frac{1}{C}\left(\frac{R}{R + {r}_{C}}{i}_{L}- \frac{1}{R + {r}_{C}}{v}_{C}\right) \\ \\ {v}_{O} &= \frac{R \times {r}_{C}}{R + {r}_{C}}{i}_{L} + \frac{R}{R + {r}_{C}}{v}_{C} \end{align*}$

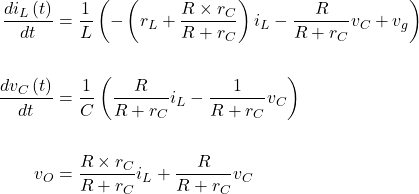
3. Transform the state equations to a compact matrix form.

During DTs

$\begin{align*} \frac{d\mathbf x\left({\mathrm{t}}\right)}{dt} &= {\mathbf A}_{1}\mathbf x(t) + {\mathbf B}_{1}\mathbf u(t) \\ \mathbf y(t) &= {\mathbf C}_{1}\mathbf x(t) + {\mathbf E}_{1}\mathbf u(t) \end{align*}$

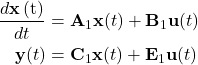
$\begin{align*} \frac{d}{dt}\left[\begin{array}{cc} {i}_{L}\left(t\right) \\ {v}_{C}\left(t\right) \\ \end{array}\right] &= \left[\begin{array}{cc} - \frac{{r}_{L}}{L} & 0 \\ \\ 0 & - \frac{1}{C\left(R + {r}_{C}\right)} \\ \end{array}\right]\left[\begin{array}{cc} {i}_{L}\left(t\right) \\ {v}_{C}\left(t\right) \\ \end{array}\right] + \left[\begin{array}{cc} \frac{1}{L} \\ 0 \\ \end{array}\right]\left[\begin{array}{cc} {v}_{g}\left(t\right) \\ \end{array}\right] \\ \\ \left[\begin{array}{cc} {v}_{O}\left(t\right) \\ \end{array}\right] &= \left[\begin{array}{cc} 0 & \frac{R}{R + {r}_{C}} \\ \end{array}\right]\left[\begin{array}{cc} {i}_{L}\left(t\right) \\ {v}_{C}\left(t\right) \\ \end{array}\right] + \left[\begin{array}{cc} 0 \\ \end{array}\right] \left[\begin{array}{cc} {v}_{g}\left(t\right) \\ \end{array}\right] \end{align*}$

During (1-D)Ts

$\begin{align*} \frac{d\mathbf x\left({\mathrm{t}}\right)}{dt} &= {\mathbf A}_{2}\mathbf x(t) + {\mathbf B}_{2}\mathbf u(t) \\ \mathbf y(t) &= {\mathbf C}_{2}\mathbf x(t) + {\mathbf E}_{2}\mathbf u(t) \end{align*}$

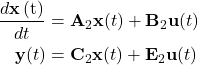
$\begin{align*} \frac{d}{dt}\left[\begin{array}{cc} {i}_{L}\left(t\right) \\ {v}_{C}\left(t\right) \\ \end{array}\right] &= \left[\begin{array}{cc} - \left(\frac{{r}_{L}}{L} + \frac{R \times {r}_{C}}{L\left(R + {r}_{C}\right)}\right) & - \frac{R \times {r}_{C}}{L\left(R + {r}_{C}\right)} \\ \\ \frac{R}{C\left(R + {r}_{C}\right)} & - \frac{1}{C\left(R + {r}_{C}\right)} \\ \end{array}\right]\left[\begin{array}{cc} {i}_{L}\left(t\right) \\ {v}_{C}\left(t\right) \\ \end{array}\right] + \left[\begin{array}{cc} \frac{1}{L} \\ 0 \\ \end{array}\right]\left[\begin{array}{cc} {v}_{g}\left(t\right) \\ \end{array}\right] \\ \\ \left[\begin{array}{center center} {v}_{O}\left(t\right) \\ \end{array}\right] &= \left[\begin{array}{center center} \frac{R \times {r}_{C}}{R + {r}_{C}} & \frac{R}{R + {r}_{C}} \\ \end{array}\right]\left[\begin{array}{center center} {i}_{L}\left(t\right) \\ {v}_{C}\left(t\right) \\ \end{array}\right] + \left[\begin{array}{center center} 0 \\ \end{array}\right] \left[\begin{array}{center center} {v}_{g}\left(t\right) \\ \end{array}\right] \end{align*}$

4. Now, we will do the averaging of the state spaces, by multiplying the matrices A1, B1, C1, and E1 with D and multiplying A2, B2, C2, and E2 with (1-D).

$\begin{align*} \mathbf A &= {\mathbf A}_{1}\mathbf D + {\mathbf A}_{2}(1 - \mathbf D) = {\small\left[\begin{array}{cc} - \frac{{r}_{L}}{L}D & 0 \\ \\ 0 & - \frac{1}{C\left(R + {r}_{C}\right)}D \\ \end{array}\right] + \left[\begin{array}{cc} - \left(\frac{{r}_{L}}{L} + \frac{R \times {r}_{C}}{L\left(R + {r}_{C}\right)}\right)\left(1 - D\right) & - \frac{R \times {r}_{C}}{L\left(R + {r}_{C}\right)}\left(1 - D\right) \\ \\ \frac{R}{C\left(R + {r}_{C}\right)}\left(1 - D\right) & - \frac{1}{C\left(R + {r}_{C}\right)}\left(1 - D\right) \\ \end{array}\right]} \\ \\ \mathbf B &= {\mathbf B}_{1}\mathbf D + {\mathbf B}_{2}(1 - \mathbf D) = \left[\begin{array}{cc} \frac{1}{L}D \\ 0 \\ \end{array}\right] + \left[\begin{array}{cc} \frac{1}{L}\left(1 - D\right) \\ 0 \\ \end{array}\right] \\ \\ \mathbf C &= {\mathbf C}_{1}\mathbf D + {\mathbf C}_{2}(1 - \mathbf D) = \left[\begin{array}{cc} 0 & \frac{R}{R + {r}_{C}}D \\ \end{array}\right] + \left[\begin{array}{cc} \frac{R \times {r}_{C}}{R + {r}_{C}}\left(1 - D\right) & \frac{R}{R + {r}_{C}} \\ \end{array}\left(1 - D\right)\right] \\ \\ \mathbf E &= {\mathbf E}_{1}\mathbf D + {\mathbf E}_{2}(1- \mathbf D) = \left[\begin{array}{cc} 0 \\ \end{array}\right]D + \left[\begin{array}{cc} 0 \\ \end{array}\right]\left(1- D\right) = 0 \end{align*}$

5. Now, we can use the averaging result to calculate the steady-state values. As we know, during steady-state the inductor current and the capacitor voltage are constant (dI_L/dt = 0, dV_C/dt =0). In that case, we can solve the equations for the steady-state inductor current (I_L) and steady-state capacitor voltage (V_C).

$\begin{align*} 0 &= \mathbf A\mathbf X + \mathbf B\mathbf U \\ \mathbf Y &= \mathbf C\mathbf X + \mathbf E\mathbf U \end{align*}$

We can re-arrange the first line to calculate matrix X which will give us the equations for I_L and V_C. After that, we substitute the value of X into matrix Y to get the output equation V_O.

$\begin{align*} \mathbf X &= - \mathbf A^{ - 1}\mathbf B\mathbf U \\ \mathbf Y &= \left[ - \mathbf C\mathbf A^{ - 1}\mathbf B\mathbf U\right] \end{align*}$

We will solve those equations using algebra linear. MATLAB is the perfect tool to do this because it can calculate it correctly.

$\begin{align*} \left[\begin{array}{center center} {I}_{L} \\ {V}_{C} \\ \end{array}\right] &= \left[\begin{array}{cc} \frac{{{\mathrm{V}}}_{{\mathrm{G}}}\left({\mathrm{C}} + {\mathrm{R}} + {{\mathrm{r}}}_{{\mathrm{C}}}{\mathrm{D}} - {\mathrm{CD}}\right)}{{{\mathrm{r}}}_{{\mathrm{L}}}{\mathrm{C}} + {{\mathrm{r}}}_{{\mathrm{L}}}{\mathrm{R}} - 2{{\mathrm{DR}}}^2 + {\mathrm{R}}^2 + {\mathrm{D}}^2{\mathrm{R}}^2 + {\mathrm{CR}} - 2{\mathrm{CDR}} - {{\mathrm{r}}}_{{\mathrm{L}}}{\mathrm{CD}} + {{\mathrm{r}}}_{{\mathrm{C}}}{\mathrm{DR}} + {{\mathrm{r}}}_{{\mathrm{C}}}{{\mathrm{r}}}_{{\mathrm{L}}}{\mathrm{D}} + {{\mathrm{CD}}}^2{\mathrm{R}} - {{\mathrm{r}}}_{{\mathrm{C}}}{\mathrm{D}}^2{\mathrm{R}}} \\ \\ \frac{ - \left({{\mathrm{RV}}}_{{\mathrm{G}}}\left({\mathrm{D}} - 1\right)\left({\mathrm{C}} + {\mathrm{R}}\right)\right)}{{{\mathrm{r}}}_{{\mathrm{L}}}{\mathrm{C}} + {{\mathrm{r}}}_{{\mathrm{L}}}{\mathrm{R}} + 2{{\mathrm{DR}}}^2 + {\mathrm{R}}^2 + {\mathrm{D}}^2{\mathrm{R}}^2 + {\mathrm{CR}} - 2{\mathrm{CDR}} - {{\mathrm{r}}}_{{\mathrm{L}}}{\mathrm{CD}} + {{\mathrm{r}}}_{{\mathrm{C}}}{\mathrm{DR}} + {{\mathrm{r}}}_{{\mathrm{C}}}{{\mathrm{r}}}_{{\mathrm{L}}}{\mathrm{D}} + {{\mathrm{CD}}}^2{\mathrm{R}} - {{\mathrm{r}}}_{{\mathrm{C}}}{\mathrm{D}}^2{\mathrm{R}}} \\ \end{array}\right] \\ \\ \left[\begin{array}{center center} {V}_{O} \\ \end{array}\right] &= \left[\begin{array}{center center} \frac{ - R{V}_{G}\left(D - 1\right)\left({r}_{C}C + {r}_{C}R + {{r}_{C}}^2D + R^2 + CR - {r}_{C}CD\right)}{\left(R + {r}_{C}\right)\left({r}_{L}C + {r}_{L}R - 2DR^2 + R^2 + D^2R^2 + CR - 2CDR - {r}_{L}CD + {r}_{C}DR + {r}_{C}{r}_{L}D + CD^2R - {r}_{C}D^2R\right)} \\ \end{array}\right] \end{align*}$

6. Calculating the averaged small-signal state-space model. The small signal model can be obtained by adding small perturbations to the averaged state-space model

$\begin{align*} \frac{d}{dt}\left[\boldsymbol X + \widehat{\boldsymbol x}\right] &= \footnotesize\left[\begin{array}{cc} {A}_{1}\left(\boldsymbol D + \widehat{\boldsymbol d}\right) + {A}_{2}\left(1 - \left(\boldsymbol D + \widehat{\boldsymbol d}\right)\right) \\ \end{array}\right]\left[\begin{array}{cc} \boldsymbol X + \widehat{\boldsymbol x} \\ \end{array}\right] + \left[\begin{array}{cc} {B}_{1}\left(\boldsymbol D + \widehat{\boldsymbol d}\right) + {B}_{2}\left(1 - \left(\boldsymbol D + \widehat{\boldsymbol d}\right)\right) \\ \end{array}\right]\left[\begin{array}{cc} \boldsymbol U + \widehat{\boldsymbol u} \\ \end{array}\right] \\ \\ \left[{\boldsymbol V}_{\boldsymbol O} + {\widehat{v}}_{o}\right] &= \footnotesize\left[\begin{array}{center center} {C}_{1}\left(\boldsymbol D + \widehat{\boldsymbol d}\right) + {C}_{2}\left(1- \left(\boldsymbol D + \widehat{\boldsymbol d}\right)\right) \\ \end{array}\right]\left[\begin{array}{center center} \boldsymbol X + \widehat{\boldsymbol x} \\ \end{array}\right] + \left[\begin{array}{center center} {E}_{1}\left(\boldsymbol D + \widehat{\boldsymbol d}\right) + {E}_{2}\left(1- \left(\boldsymbol D + \widehat{\boldsymbol d}\right)\right) \\ \end{array}\right]\left[\begin{array}{center center} \boldsymbol U + \widehat{\boldsymbol u} \\ \end{array}\right] \end{align*}$

The capital X on the left side can be ignored because during steady-state or DC there is no signal fluctuation. On the right side, all of the DC components and the high-order components will be neglected. At the end, we will have the small signal components only.

$\begin{align*} \frac{d}{dt}\left[X + \widehat{x}\right] = \footnotesize\left[{A}_{1}DX + {A}_{1}X\widehat{d} + {A}_{2}X - {A}_{2}DX - {A}_{2}X\widehat{d} + {A}_{1}D\widehat{x} + {A}_{1}\widehat{x}\widehat{d} + {A}_{2}\widehat{x} - {A}_{2}D\widehat{x} - {A}_{2}\widehat{x}\widehat{d}\right] \\ + \left[{B}_{1}DU + {B}_{1}U\widehat{d} + {B}_{2}U - {B}_{2}DU - {B}_{2}U\widehat{d} + {B}_{1}D\widehat{u} + {B}_{1}\widehat{u}\widehat{d} + {B}_{2}\widehat{u} - {B}_{2}D\widehat{u} - {B}_{2}\widehat{u}\widehat{d}\right] \\ \frac{d}{dt}\left[\widehat{x}\right] = \left[{A}_{1}X\widehat{d} - {A}_{2}X\widehat{d} + {A}_{1}D\widehat{x} + {A}_{2}\widehat{x} - {A}_{2}D\widehat{x}\right] + \left[{B}_{1}U\widehat{d} - {B}_{2}U\widehat{d} + {B}_{1}D\widehat{u} + {B}_{2}\widehat{u} - {B}_{2}D\widehat{u}\right] \end{align*}$

$\begin{align*} \left[{V}_{O} + {\widehat{v}}_{o}\right] = \left[{C}_{1}DX + {C}_{1}X\widehat{d} + {C}_{2}X- {C}_{2}DX- {C}_{2}X\widehat{d} + {C}_{1}D\widehat{x} + {C}_{1}\widehat{x}\widehat{d} + {C}_{2}\widehat{x}- {C}_{2}D\widehat{x}- {C}_{2}\widehat{x}\widehat{d}\right] \\ + \left[{E}_{1}DU + {E}_{1}U\widehat{d} + {E}_{2}U- {E}_{2}DU- {E}_{2}U\widehat{d} + {E}_{1}D\widehat{u} + {E}_{1}\widehat{u}\widehat{d} + {E}_{2}\widehat{u}- {E}_{2}D\widehat{u}- {E}_{2}\widehat{u}\widehat{d}\right] \\ \left[{\widehat{v}}_{o}\right] = \left[{C}_{1}X\widehat{d}- {C}_{2}X\widehat{d} + {C}_{1}D\widehat{x} + {C}_{2}\widehat{x}- {C}_{2}D\widehat{x}\right] + \left[{E}_{1}U\widehat{d}- {E}_{2}U\widehat{d} + {E}_{1}D\widehat{u} + {E}_{2}\widehat{u}- {E}_{2}D\widehat{u}\right] \end{align*}$

After removing all of the DC and high-order components, then we do a little bit of simplification so the equation will look like as shown below.

Please remember the previous equation!

A = A₁D + A₂(1-D),
B = B₁D + B₂(1-D),
C = C₁D + C₂(1-D),
E = E₁D + E₂(1-D).

At this point, we will introduce another as a result of adding a small perturbation to the duty cycle,

F = A₁X+ B₁U- (A₂X + B₂U) and
G = C₁X+ E₁U- (C₂X + E₂U)

$\begin{align*} \frac{d}{dt}\left[\widehat{x}\right] &= \left[{A}_{1}D\widehat{x} + {A}_{2}(1 - D)\widehat{x} + {B}_{1}D\widehat{u} + {B}_{2}(1 - D)\widehat{u} + {A}_{1}X\widehat{d} + {B}_{1}U\widehat{d}- {A}_{2}X\widehat{d}- {B}_{2}U\widehat{d}\right] \\ \frac{d}{dt}\left[\widehat{x}\right] &= A\widehat{x} + B\widehat{u} + \underset{F\widehat{d}}{\underbrace{({A}_{1}X + {B}_{1}U)\widehat{d}- \left({A}_{2}X + {B}_{2}U\right)\widehat{d}}} = \boldsymbol A\widehat{\boldsymbol x} + \boldsymbol B\widehat{\boldsymbol u} + \boldsymbol F\widehat{\boldsymbol d} \\ \\ \left[{\widehat{v}}_{o}\right] &= \left[{C}_{1}D\widehat{x} + {C}_{2}(1- D)\widehat{x} + {E}_{1}D\widehat{u} + {E}_{2}(1- D)\widehat{u} + {C}_{1}X\widehat{d} + {E}_{1}U\widehat{d}- {C}_{2}X\widehat{d}- {E}_{2}U\widehat{d}\right] \\ \left[{\widehat{v}}_{o}\right] &= C\widehat{x} + E\widehat{u} + \underset{G\widehat{d}}{\underbrace{({C}_{1}X + {E}_{1}U)\widehat{d}- \left({C}_{2}X + {E}_{2}U\right)\widehat{d}}} = \boldsymbol C\widehat{\boldsymbol x} + \boldsymbol E\widehat{\boldsymbol u} + \boldsymbol G\widehat{\boldsymbol d} \end{align*}$

7. Next, we will do the Laplace transformation on these two matrices.

$\begin{align*} s\widehat{x}\left(s\right) &= \boldsymbol A\widehat{\boldsymbol x}\left(s\right) + \boldsymbol B\widehat{\boldsymbol u}\left(s\right) + \boldsymbol F\widehat{\boldsymbol d}\left(s\right) \\ sI\widehat{x}\left(s\right) - A\widehat{x}\left(s\right) &= B\widehat{u}\left(s\right) + F\widehat{d}\left(s\right) \\ (sI - A)\widehat{x}\left(s\right) &= B\widehat{u}\left(s\right) + F\widehat{d}\left(s\right) \\ \widehat{x}\left(s\right) &= {(sI - A)}^{ - 1}B\widehat{u}\left(s\right) + {(sI - A)}^{ - 1}F\widehat{d}\left(s\right) \\ \\ {\widehat{v}}_{o}\left(s\right) &= \boldsymbol C\widehat{\boldsymbol x}\left(s\right) + \boldsymbol E\widehat{\boldsymbol u}\left(s\right) + \boldsymbol G\widehat{\boldsymbol d}\left(s\right) \\ {\widehat{v}}_{o}\left(s\right) &= \boldsymbol C\left((sI- A)^{- 1}B\widehat{u}\left(s\right) + (sI- A)^{- 1}F\widehat{d}\left(s\right)\right) + \boldsymbol E\widehat{\boldsymbol u}\left(s\right) + \boldsymbol G\widehat{\boldsymbol d}\left(s\right) \\ {\widehat{v}}_{o}\left(s\right) &= C(sI- A)^{- 1}B\widehat{u}\left(s\right) + E\widehat{u}\left(s\right) + C(sI- A)^{- 1}F\widehat{d}\left(s\right) + G\widehat{d}\left(s\right) \\ \\ {\widehat{v}}_{o}\left(s\right) &= (C(sI- A)^{- 1}B + E)\widehat{u}\left(s\right) + (C(sI- A)^{- 1}F + G)\widehat{d}\left(s\right) \end{align*}$

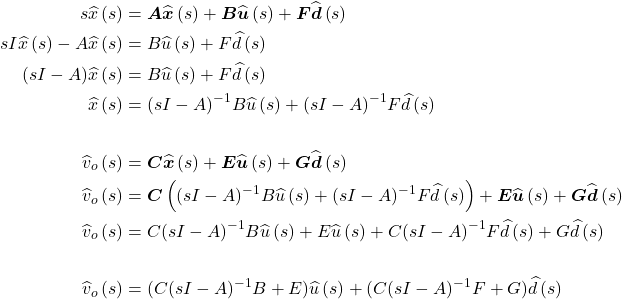
As we can see from the equation above. The output Vo is expressed on input variables, duty cycle (d(s)), and input voltage (u(s)). The control-to-output transfer function can be calculated by setting the input voltage u(s) to 0. Finally, the transfer function is

$\begin{align*} {\frac{{\widehat{v}}_{o}\left(s\right)}{\widehat{d}\left(s\right)}}_{\widehat{u} = 0}^{} = (C(sI- A)^{- 1}F + G) \\ \\ {\frac{{\widehat{v}}_{o}\left(s\right)}{\widehat{u}\left(s\right)}}_{\widehat{d} = 0}^{} = (C(sI- A)^{- 1}B + E) \end{align*}$

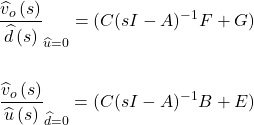
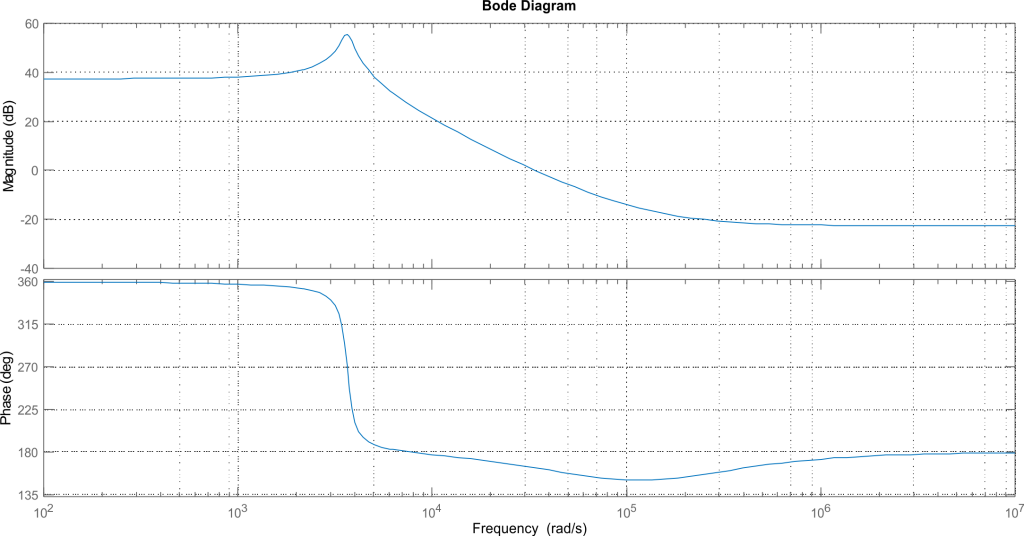
To make it easy we will use MATLAB to calculate and then plot it into a Bode plot.

MATLAB source code

% ===========================================================
%==================== 28/12/2023 ===========================
% ===========================================================

clc
clear all
close all
clear

%========= Component Values and Input Parameters ===========
% ===========================================================
VO_ = 30; % Output voltage
D_ = 0.6; % Duty cycle
VG_ = 12; % Input voltage
C_ = 100e-6; % Capacitor
rC_ = 50e-3; % Capacitor ESR
L_ = 120e-6; % Indcutor
rL_ = 10e-3; % Indcutor ESR
R_ = 50; % Output load

syms vg rg d rL L rC C R vC iL rds rD vD D IL VC VG VD s

%%%%%%%%%%%%%%%%%%%% STEP_1 %%%%%%%%%%%%%%%%%%%%
% Identify the amount of capacitor and the inductor on the DC-DC converter circuit.
% Each of these energy storage elements will be the space vector of the matrix.

%%%%%%%%%%%%%%%%%%%% STEP_2 %%%%%%%%%%%%%%%%%%%%
% Write down the equation for each state vector for each half cycle.

%%%%%%%%%%%%%%%%%%%% STEP_3 %%%%%%%%%%%%%%%%%%%%
% Transform the state equations to a compact matrix form.
% ___________during DTs______________.
%
% d[x]/dt = A1*x(t) + B1*u(t)
% y1(t) = C1*x(t) + E1*u(t)
%
% ___________during (1-D)Ts______________
%
% d[x]/dt = A2*x(t) + B2*u(t)
% y2(t) = C2*x(t) + E2*u(t)
%
% Matrix x(t) consists of the inductor current (iL) and capacitor voltage (vC)
% Matrix u(t) consists of input/controllable parameters
% e.g. input voltage (vg), input current(ig),
% Matrix y(t) consists of output/ control target parameters
% e.g. output voltage (vo) and output current (io).

%_________Transforming the equations to matrices___________.

A1 = [-(rL)/L 0;
0 -1/(C*(R+C))];

A2 = [-(rL+(R*rC)/(R+rC))/L -(R/(R+rC))/L;
(R/(R+rC))/C -(1/(R+rC))/C];

B1 = [1/L;
0];

B2 = [1/L;
0];

C1 = [0 R/(R+rC)];

C2 = [R*rC/(R+rC) R/(R+rC)];

E1 =[0];

E2 = [0];

X = [IL;
VC];

U = [VG];

%%%%%%%%%%%%%%%%%%%% STEP_4 %%%%%%%%%%%%%%%%%%%%
% Calculating the steady-state operating point
% It is done by multiplying the first half-cycle matrices (A1, B1, C1, E1) with D
% Then multiplying the second half-cycle matrices (A2, B2, C2, E2) with (1-D).
%
% ____note____
% The MATLAB function “simplify” will do some algebraic simplifications after finishing %calculation.

A = simplify(D*A1 + (1-D)*A2);
B = simplify(D*B1 + (1-D)*B2);
CC =simplify(D*C1 + (1-D)*C2);
E = simplify(D*E1 + (1-D)*E2);

%%%%%%%%%%%%%%%%%%%% STEP_5 %%%%%%%%%%%%%%%%%%%%
% During steady-state the inductor current and the capacitor voltage are
% constant (diL/dt = 0, dvC/dt =0)
% So we can write the matrices to something like below
% ________________________________________
% _____ 0 = AX + BU ____
% _____ Y = CX +EU ____
% ________________________________________
%
% Moving the AX to the left side, -AX = BU
% Isolating X so we can get X = -inv(A)BU
% Finally, we substitute X to Y equation
% Y = C(-inv(A)BU) + EU or we write as Y = (-Cinv(A)B +E)U
% ___________________________________________________
% _____ X = -inv(A)BU ____
% _____ Y = C(-inv(A)BU) +EU ____
% __________________________________________________
%

DC_Solution_X = -inv(A)*B*U ;
DC_Solution_Y = -CC*inv(A)*B*U + E*U ; % we name the matrix as CC in order to distinguish %matrix C and capacitor C

disp(‘Operating point of converter’)
disp(‘————————-‘)
disp(‘IL(A)=’)
disp(simplify(DC_Solution_X(1,1)))
disp(‘VC(V)=’)
disp(simplify(DC_Solution_X(2,1)))
disp(‘VO(V)=’)
disp(simplify(DC_Solution_Y))
disp(‘VO_simplify(V)=’)
disp(simplify(subs((DC_Solution_Y),[rL rC],[0 0])))
disp(‘—————————-‘)

%%%%%%%%%%%%%%%%%%%% STEP_6 %%%%%%%%%%%%%%%%%%%%
% Calculating the averaged small-signal state-space model
% The small signal model can be obtained by adding small perturbations to the averaged %state-space model
% Please refer to the post on the website,
% to know how the small perturbation calculations are done for this converter
%
% ________Calculating the additional matrices (F and G) due to small perturbation on the duty cycle variable
%
% !!!!!!!!!___The matrix Xx consists of DC solution for IL and VC.___!!!!!!!!

Xx = DC_Solution_X ;

F = A1*Xx + B1*U – (A2*Xx + B2*U);
G = C1*Xx + E1*U – (C2*Xx + E2*U);

% Obtaining the control-to-output (V_od) transfer function by setting the input voltage u(s) % to 0
% Obtaining the input-to-output (V_oi) transfer function by setting the duty-cycle d(s) to 0
% ______________________________________________________
% _____ V_od(s) = C inv(sI-A)F + G ____
% _____ V_oi(s) = C inv(sI-A)B + E ____
% ______________________________________________________

I = eye(2); % identity matrix

Vo_d = simplify((CC*(inv(s*I-A))*F + G),’Steps’,50) % The transfer function equation in “VG, % R, D, L, C, rC, rL, s”

Vo_d_ = simplify(subs((CC*(inv(s*I-A))*F + G),[VG D R L C rL rC],[VG_ D_ R_ L_ C_ rL_ rC_]),’Steps’,50)

%%%%%%%%%%%%%%%%%%%% STEP_7 %%%%%%%%%%%%%%%%%%%%
% Plotting the transfer function into a Bode Plot

s=tf(‘s’);
opts = bodeoptions (‘cstprefs’);
opts.FreqUnits = ‘Hz’;
Vo_d__ =- ((1665418330830000000000*s)/334250917 – 166625808533983600000000000000/334585167917)/(500501001*s^2 + 225101996750*s + 6685018340000000) – 25015020000/334585167917; % manually place the Vo_d transfer func. here
bode(Vo_d__)
grid on
grid minor

%======================= END ====================================
%================================================================.

Deriving the Small-Signal Model of the Boost Converter using State-Space Averaging

Comments

Leave a Reply Cancel reply