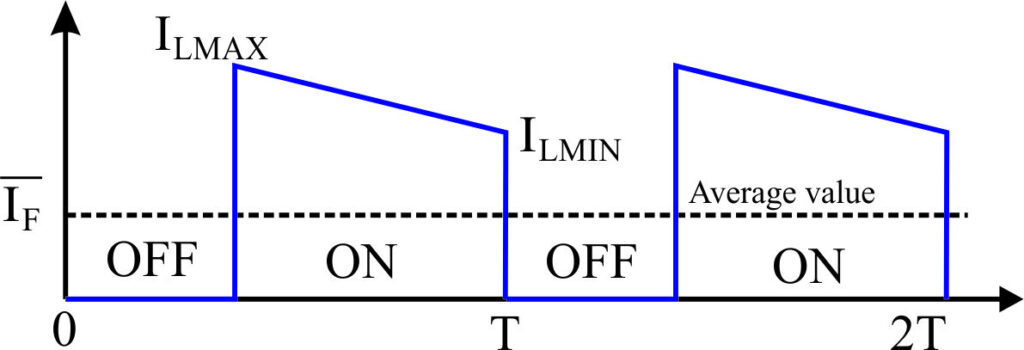
The figure above shows the diode current waveform at the steady state. The average value of this current waveform can be calculated as the area during the ON state of the diode. The area below the waveform is equal to the area of a trapezoid.
![\[{I}_{F} = \frac{\left({I}_{Lmin} + {I}_{Lmax}\right) \cdot {t}_{ON\underline Diode}}{2 \cdot T}\]](https://sawitray.com/wp-content/ql-cache/quicklatex.com-09a71ae44b2cff1f1c311cfadca4f6fd_l3.png "Rendered by QuickLaTeX.com")
![\[{I}_{F} = \frac{\left(\left({I}_{Lmax} - \Delta{I}_{L}\right) + {I}_{Lmax}\right) \cdot \left(1 - D\right)T}{2 \cdot T} = \frac{\left(2{I}_{Lmax} - \Delta{I}_{L}\right)\left(1 - D\right)}{2}\]](https://sawitray.com/wp-content/ql-cache/quicklatex.com-cc6ed5a49b7370748479ea710a4eaef4_l3.png "Rendered by QuickLaTeX.com")
![\[{I}_{F} = \left({I}_{Lmax} - \frac{\Delta{I}_{L}}{2}\right)\left(1 - D\right) = {I}_{OUT} \cdot \left(1 - D\right)\]](https://sawitray.com/wp-content/ql-cache/quicklatex.com-caee5623f90138749dc0b7befccff4b1_l3.png "Rendered by QuickLaTeX.com")
On the last equation, if we remember the current waveform of the inductor we can understand that the difference between max. current (ILmax) and half of the ripple current (ΔIL/2) is equal to the output current (IOUT).